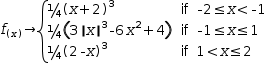2.8.2 Piecewise Expressions

A piecewise function is defined by multiple subfunctions over a common partitioned domain. In Myron, a piecewise expression implies a piecewise function if its partition specifications tile a linear domain. There are two parts to this. First, every expression implies a function as if the expression was part of a definition. That is, x^2-2⋅x+1 implies f(x)→x^2-2⋅x+1; similarly, t<u?t:u implies f(t, u)→t<u?t:u. Thus we have a function with multiple subfunctions.

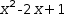
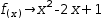
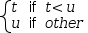
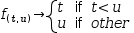
Second, if at most one partition test in a piecewise function is true for a common domain, the partitioned domains are disjoint and the piecewise function is said to tile the domain. Myron does not enforce disjoint domain tiling so not all Myron piecewise expressions are strict piecewise functions. When evaluated, overlap in partition specifications is reconciled by using the first specification that is true.

Two syntactic forms for piecewise functions are given in Figure 2.40. The keyword “if” introduces a list-like construct whose elements consist of partition.→range expression phrases. The alternative form uses the ternary ?: operator.

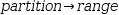
The simple function s(t)→|t|^3 can be given by the piecewise function s_3(t)→if(t≥0→t^3, t<0→-t^3). In its piecewise form, the function can be seen to be the parabola |t^3|.

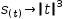
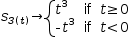
To illustrate the syntax, the input form of the example is s_3(t) → if(t≥0 → t^3, t<0 → -t^3). Being a two-way piecewise function, the example can also be expressed using the ternary ?: operator using the input s_3(t) → t≥0 ? t^3 : -t^3.

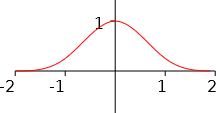
A cubic spline that expresses a bell curve (see Figure 2.41) is given by the piecewise function